ワールド "Bounded H²" を Community Labs に上げました https://t.co/1e1SaYw7s2 pic.twitter.com/ugBtWFWxe8
— phi16 (@phi16_) 2023年2月16日
ワールドが生えました。
経緯
最初のきっかけは Connecting Artifacts つながるかたち展 02 です。
いくつか負曲率曲面がおいてありました。うーんなるほど。楽しそう。
双曲平面の表示として Poincaré disk model はよく知られていますが、それをそのままVRにもっていくには「端っこが縮まなければならない」のでアバターの扱いが難しいです。
なら等長埋め込みとして 内の曲面にすればいいじゃん、というのは思いました。が、曲面の構成が明らかではありません。
世の中には Hyperbolic Crochet というものがあり、つまり編み物で (等長埋め込みとしての) 双曲平面を作るとこんな形になるということを知っていました。
逆に言えばこれを作れば良さそう。
定曲率の曲面ならその上をスムーズに移動できる、というのは昔考えたことで実際に pseudosphere 上の物理シミュレーションを組んだことがあります (懐かしい)。
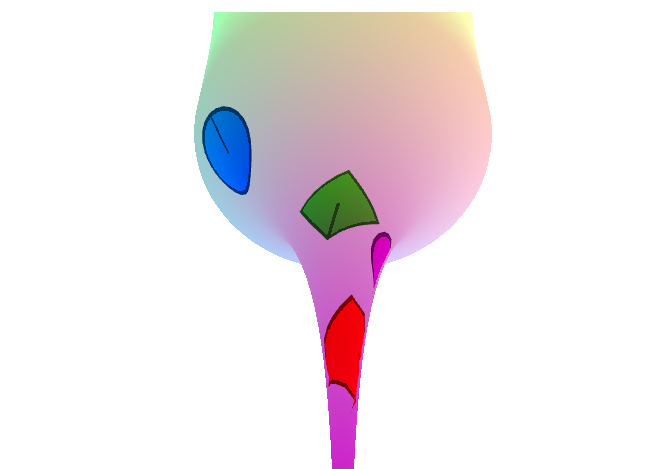
うーん楽しそうだけどどうやるかな。距離拘束を解けばまぁそれっぽくなるんかな。と思って Houdini で自前でシミュレーション (?) 書いて作ったのがこれです。
みたいものがみれた pic.twitter.com/s3PuylC2g7
— phi16 (@phi16_) 2022年11月7日
確かに「空間が滑っていく様子」が見れました。まんぞく。
でも簡素な仕組みで作ったのでプレイヤー同期とかが何もできません。ちょっとワールドとして出すには微妙でした。
とりあえず放置してたんですが。
"The Library of Hilbert"をVRChatにて公開しました。https://t.co/NE2v5fXdoN
— ねむり木 (@Name1ess_Newbie) 2023年1月6日
J.L.ボルヘス「バベルの図書館」とヒルベルト曲線のマッシュアップを試みました。
お越しの際は酔いにご注意ください。#MadeWithVRChat#VRChat#VRChat_world紹介 pic.twitter.com/jR3MGb0gn8
アーってなりました。アーって。
プレイヤー同期に必要なのは「平面上のプレイヤーの位置から、空間内の位置と姿勢を復元する仕組み」です。つくるのたいへんだな~って思ったら作られてしまいました。
道が1次元だから出来る簡略化はありそうだなと思いましたが、まぁ2次元でもなんかどうにかすればなんとかなるんじゃないかと思えました。
悔しいので頑張ろうとなりました。これが 新年のとき の気持ち。
実現を考える
VRChatにおける「プレイヤー位置が人によって異なる仕組み」は、端的に 椅子 でできています。
プレイヤーは椅子に乗ると「椅子の位置にプレイヤーが居る」ことになります。椅子を同期させなければプレイヤー位置も同期しません。
ヤッター pic.twitter.com/t2lQUiv6Ac
— phi16 (@phi16_) 2020年12月8日
昔一応検証としてやったことがあったんですが、プロジェクトどっか行ったし、複数人でうまく動いてなかったので、suzuki さんのを利用することにしました。
まぁ実際には中身見て完全に理解して今回用に自分で作った、みたいな感じです。
というわけでワールドでやらなければならないことは:
- ギミックを (VRChatの) プレイヤー位置に移動させる
- 曲面上にどうにかしてプレイヤーの椅子を配置する
- 曲面を「ギミック原点に自分が来るように」平行移動・回転させる
以上です。
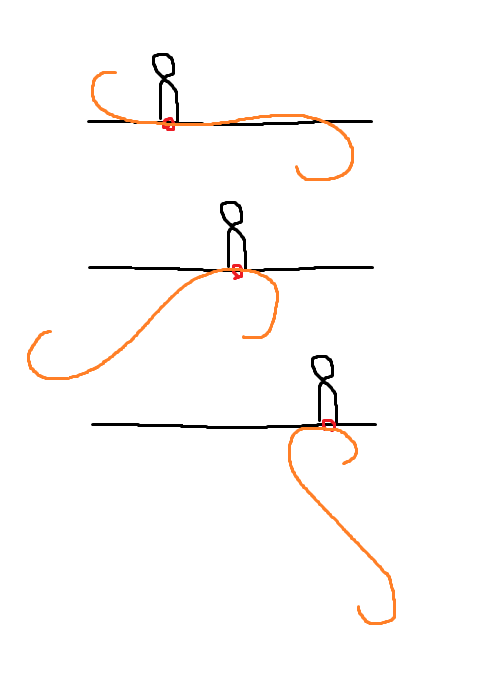
プレイヤーは Unity 的にはめちゃ広い平面を歩いているだけです。
ちなみにギミック原点に直接 pickup を入れてるので歩いても勝手に地図がついてくる。
というわけで残りの課題は「プレイヤーの位置を得る」部分だけです。
まず「曲面を歩く」ためには、曲面上の点における接空間が重要です。あと 接続 の概念。
任意の曲面を歩く場合には フレーム を局所的に動かしていくことになるのでしょう。少し移動させて、新たな法線に沿ってフレームを回転させる。自動的に holonomy もついてきます。
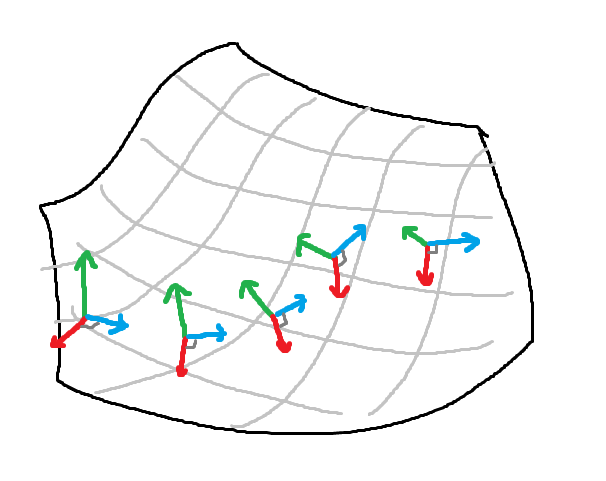
(移動方向とフレームの向きは独立しています)
その為には「曲面がどこにあるのか」を正確に知っていなければなりません。よくあるメッシュデータ (vertices/indices) は「ポリゴンの集合体」でしかなくて全然足りません。
最低でも隣接するポリゴンがわかれば常に (境界でも) 開近傍が取れるようになるので多様体っぽくなって (微分不可能なのでアレだけど) なんとかなります。SDFでも大丈夫です。
が、この話は今回は関係ありません。
今回は曲面を歩くのではなく「双曲平面を歩いていて、それが曲面として表示されている」だけです。
なので必要なのは「双曲平面を歩く方法」「双曲平面上の位置から対応する曲面上の位置を得る方法」です。接空間は微分すれば付いてきます。
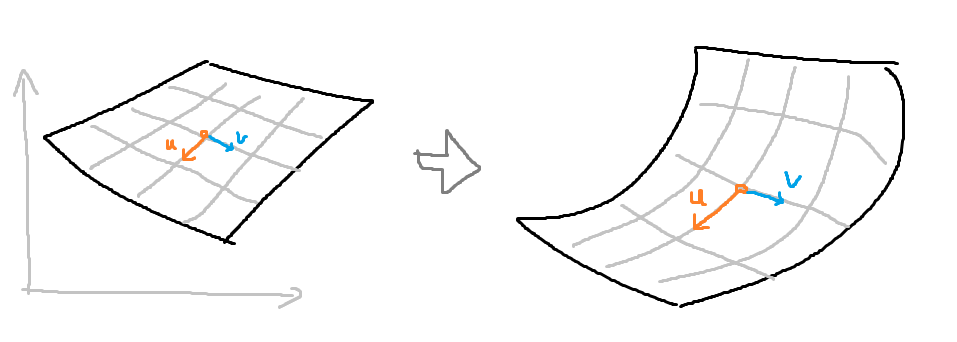
前者はさておき、後者は要は曲面をパラメータ表現できれば良い、ということです。つまりUV座標を張ればいい。
が、双曲平面なので (曲率が0じゃないので) きれいなUV展開は存在しません。そこで seam を切ります。

あとは「自分がどの区画のどの座標に居るか」「区画毎の曲面のパラメータ表現」そして「区画と区画の繋がり」がわかれば完璧です。
というわけでパネル毎の位置データがこちら。(色で空間上の位置を表現しています)
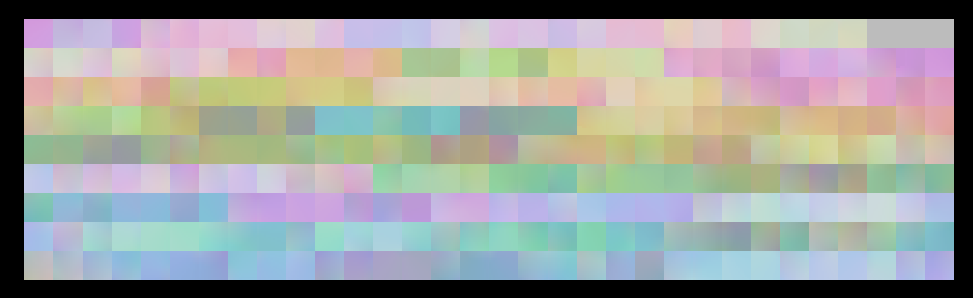
パネルの接続情報がこれ。
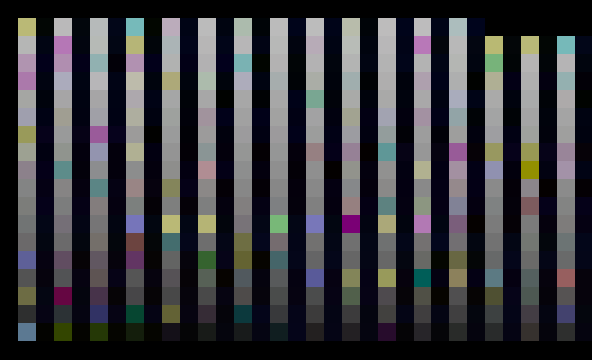
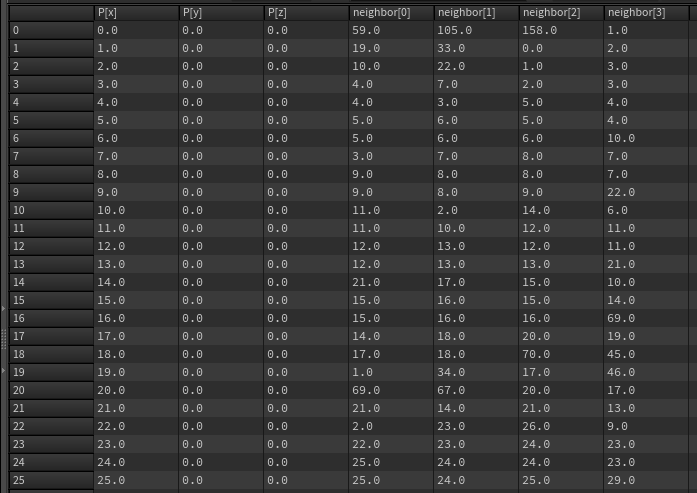
隣が居ないときは自分自身のIDを振りました。番兵ってやつですね。
これがあれば多様体っぽくなりますね。ついでに位置データを微分すれば法線が得られるので接空間も大丈夫。十分です。
曲面のつくりかた
まずベースとなるメッシュを用意します。私は Poincaré disk にしました。Poincaré disk は「等角」な投影なので、見た目の角度をそのまま使えて嬉しい。
堀川さんが Qiita に記事を書いている ので読むと作れます。が、そのままだと「各面にグリッドを張る方法」がわからなかったのと、その時は Houdini 力が全然足りなかったので C# で作っちゃいました。
グリッドを張るためには四角形が一番便利です。Poincaré disk は四角形の tessellation として構成できますが、ユークリッド空間と違って各頂点の内角は自由です (角度が狭いなら大きくなるだけ)。今回は 60°、つまり 6 つの四角形で一周する構造にしました。

グリッドの作り方は、「辺を等分割して」「対応する2点を (Poincaré disk 上) まっすぐ結ぶ円弧を描く」ことで行いました。(双曲平面内の「直線」は Poincaré disk では (無限大の半径を許す) 円になります)
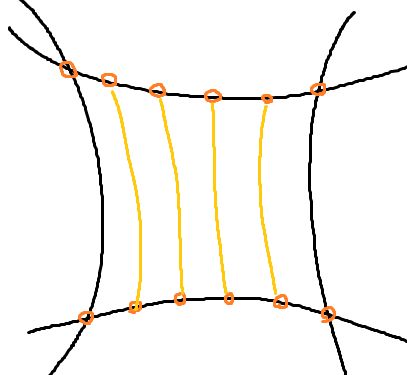
2点だと円が定まらなかったのですが、なんか「Poincaré disk 上のある点を通る直線 (円) は、その点を 反転 させた点 (p / dot(p,p)) も通る」らしかったので、なんとかなりました。
(…しかし、多分 Beltrami-Klein モデルに持っていて線形変換したほうが楽でした。計算量的にも。まぁ歪みはこっちのほうが少ないはずだけど。)
Poincaré disk 上では「中心から離れるにつれて空間が伸びていく」はずなのでポリ割はちょっと気を使いました。斜め線の方向を。

ちなみになんで 14x14 なのかというと、座標復元のときに bicubic 補間をしたかったので端っこが 1px ずつ必要だったからです。
なんやかんやあって Poincaré disk が完成します。端っこが汚かったので Boolean で切ります。半径は 0.975 になりました。

あとはこれを等長に戻すだけです。
ここでいう等長というのは Poincaré disk 上の見かけの長さではなく双曲平面の本来の長さという意味です。ありがたいことに Wikipedia に計算方法が書いてありました。
ここから隣接頂点との距離拘束を与えることができます。隣接するだけだと平ったくならない (バキバキになる) ので隣接頂点の隣接頂点まで拘束条件を入れてみました。
function float arcosh(float z) { return log(z + sqrt(z+1) * sqrt(z-1)); } function float hyperDist(vector2 p; vector2 q) { float v = 2 * length2(p-q) / (1 - length2(p)) / (1 - length2(q)); return arcosh(1 + v); } // Retrieve 0/1-hop points int nps[]; int neis[] = neighbours(0, @ptnum); for(int j=0;j<len(neis);j++) { int cands[] = neighbours(0, neis[j]); push(cands, neis[j]); for(int k=0;k<len(cands);k++) { if(cands[k] != @ptnum && find(nps, cands[k]) < 0) { push(nps, cands[k]); } } } // Save connected points information int nc = len(nps); int np[]; float nd[]; for(int i=0;i<nc;i++) { vector2 coord = point(0, "coord", nps[i]); float d = hyperDist(u@coord, coord); push(np, nps[i]); push(nd, d); } i[]@np = np; f[]@nd = nd;
後は Position Based Dynamics 的に拘束を解きます。Attribute Wrangle で。
…ぐだぐだになりました。まず激重い。
それでもなんとか動いて出来たのが最初の Hyper でした。でもメッシュに自己交差が入っていて「歩く」にはさすがに邪魔です。
というわけで悩んでいましたが、Vellum がすべてを解決してくれました。
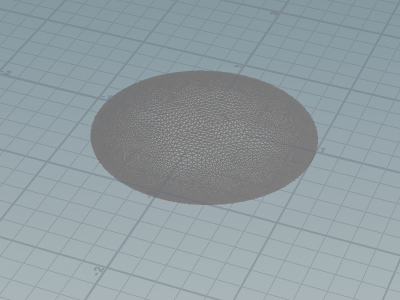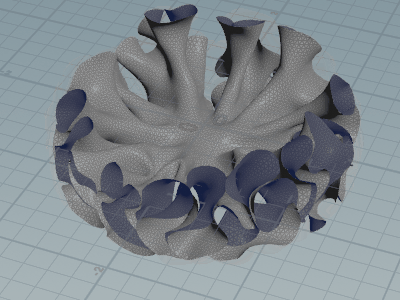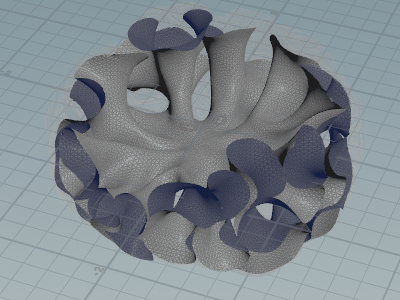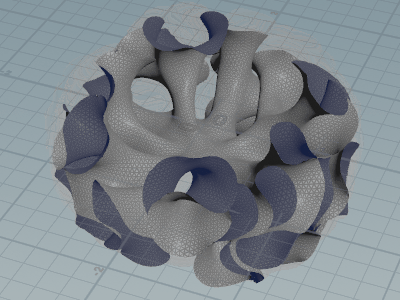
適当に Cloth を付けた後、constraint geometry を直接弄ります。
function float arcosh(float z) { return log(z + sqrt(z+1) * sqrt(z-1)); } function float hyperDist(vector2 p; vector2 q) { float v = 2 * length2(p-q) / (1 - length2(p)) / (1 - length2(q)); return arcosh(1 + v); } int ps[] = primpoints(0, @primnum); vector2 p = point(1, "coord", ps[0]); vector2 q = point(1, "coord", ps[1]); f@restlength = f@restlengthorig = hyperDist(p, q) * 0.3;
はい。これでうまくいきました。
(ちなみに後で lox9973 さんに教えてもらいましたが、堀川さんがほぼ同じようなことをやってました)
ただちょっと端っこがじゃぎじゃぎしちゃった (境界に関する拘束が足りない) ので、それは自前のシミュレーションでちょっと直しました。

無駄にはならなかった…! (まぁぶっちゃけ Vellum でちゃんと拘束生やしたほうが良かったのでは?という気はあるが)
双曲平面を歩く
残るは双曲平面の扱いだけです。
平面ということは位置を2つの数値で (概ね) 決定できるということです。双曲平面に座標を与える方法はいろいろあります。
- Poincaré disk model: 等角。直線は円になったりする。
- Beltrami-Klein model: 線形。直線は直線。
- Hyperboloid model: 変換を行列で表せて便利。3つの数字と1つの拘束で座標を表します。
この違いはアレです、地図の図法の違いみたいなもんです (ステレオ投影, 心射図法, 球上の3次元座標を直接使う方式)。お互いに変換が可能。この動画 めちゃ良いです。
今回は私の好みで Poincaré disk 上の座標を直接使いました (まぁメッシュもそうやって作ってるし)。ただこれによって変換の扱いが大変にしんどいことになります。
ちなみに、Poincaré disk 上の座標ということは「端っこに行けば行くほど縮む」ということです。中心 から右に少し進むと
くらいになりますが、
から右に少し進んでも
くらいにしかなりません。世界がものすごい圧縮されてるのです。
浮動小数点数には精度の限界があります。0 付近はかなり細かいんですが 1 付近では float だと 23bit 程度しかありません。これは 0.0000001 を区別できないくらい () です。だから Poincaré disk の範囲を制限しないとまずいのです。
今回はメッシュの構造的に半径を 0.975 に制限してしまったので、ついでにプレイヤーの移動範囲も同じく 0.975 に制限することにしました。「範囲を制限された双曲平面」、これが名前の Bounded H² の由来です (双曲平面を と書くのです)。
Poincaré disk 上の座標は Gyrovector space を成すことが知られています (Möbius gyrovector space)。この Gyrovector space というのはまぁ Vector space (線形空間) の「亜種」なんですが、まぁ亜種にしてもひどいです。
足し算が可換でないどころか、結合的ですらありません。まぁ"直感的"に書いたらバグる、ということです。
まぁそれは空間構造的には正しいです。正しいから演算が歪むのです。…でもこの現象は Hyperboloid model では起きません。なんでかな~と思ったんですが、おそらく「回転」がその原因なのでしょう。
Gyrovector 上の加算 (Gyroaddition) が「どれくらい結合的でないか」を示す指標が Gyrator です。こいつは Möbius gyrovector space においてはどうやら回転に対応しているようです。つまり「足し算をすると、空間が回る」のです。holonomy っぽい。
逆に言えば「回転を加味した状態で空間に変換を噛ます分には結合的」なのではないかと思います。そこまで丁寧にやったわけではないので知らんけど。
実際、先程書いたように曲面の上を歩くにはフレーム (Z軸がどっちを向いているか) を維持していかないといけません。なのでどうせ「位置と回転」を一緒に使うことにはなります。
というわけで位置変換の方法が定まりました。
こうです。めんどくさいですね。
今後「適切に」 を使って座標をくるくる回す必要が出てきます。もう私は諦めて主に勘で書いちゃいました。
さて、まず毎フレーム Unity 上での移動量を計算し、それを適切に双曲平面上の変換に直す必要があります。4m 横に動く変換が だとしても、8m 横に動く変換はもちろん
ではありません (長さが 1 以上には絶対にならない)。
になります。
これについても単純な式が Wikipedia に書いてありました。 して
すればいいらしいです。
というわけでなんとかなります。
Vector2 rotRet = new Vector2(1,0); Vector2 GyroAdd(Vector2 z, Vector2 a) { Vector2 deno = new Vector2(1,0) + MulC(a, ConjC(z)); Vector2 nume = a + z; Vector2 ret = MulC(nume, InvC(deno)); rotRet = MulC(ConjC(deno), InvC(deno)); return ret; } void Update() { Vector3 pp = localPlayer.GetPosition(); Vector3 p = pp - prevPos; Vector2 d = new Vector2(p.x, p.z); float l = d.magnitude; if(l > eps) { Vector2 dd = d.normalized * HyperLength(l); // here! hyperPos = GyroAdd(dd, hyperPos); hyperRot = MulC(rotRet /* gyrator */, hyperRot); // complex multiplication } prevPos = pp; }
ここまでやると初期の Hyper の方が出来ます。が、これに加えて「自分が曲面を歩く」「他プレイヤーの位置を計算する」ことをしなければなりません。
とは言え道具はもう揃っています。相対位置を計算したいなら逆変換を掛ければいいのです。
最初は「双曲平面上の座標」と「メッシュ原点の双曲平面上の座標」を保持しようと思っていました。が、なんか結合性の問題でうまくいきませんでした (多分方法はあると思うんですが…)。
なので「メッシュ原点から見た、双曲平面上の座標」と「メッシュ原点の双曲平面上の座標」を保持することにしました。
ごちゃごちゃしていてわかりにくいですが、要は「ワールド座標とカメラの位置で管理しようとしたがうまくいかなかったので、カメラから見た座標とカメラの位置を管理するようにした」ということです。
なんやかんやあってうまくいきました。試行錯誤にめっちゃ時間掛かってる。
(カメラの座標は素直に (???) 動かせばいいんですが、カメラから見た座標は「逆向き」に動かす必要性みたいなのが出てくる)
Vector2 pos, rot; // ワールド座標系 Vector2 visualPos, visualRot; // カメラの位置 Vector2 viewPos, viewRot; // カメラから見た座標系 void Move(Vector2 visualDiff, Vector2 viewDiff) { // visual visualPos = GyroAdd(-pos, visualPos); visualRot = MulC(rotRet, visualRot); visualPos = GyroAdd(MulC(rot, visualDiff), visualPos); visualRot = MulC(rotRet, visualRot); visualPos = GyroAdd(pos, visualPos); visualRot = MulC(rotRet, visualRot).normalized; // view viewPos = GyroAdd(viewPos, MulC(viewRot, viewDiff)); viewot = MulC(rotRet, viewRot).normalized; // world pos = GyroAdd(visualPos, MulC(visualRot, viewPos)); rot = MulC(rotRet, MulC(visualRot, viewRot)); }
正直自分でよくわかってません。とりあえず動いてます。
さてまぁ、そうすると「pos, rot を同期させれば良い」「他人の pos, rot を visualPos, visualRot で逆変換すると表示すべき座標が手に入る」ということになります。
ちなみに位置関係によっては他プレイヤーは半径 0.975 の範囲を容易に越えうるので、実はその場合は (0, -200, 0) に飛ばしてます。
というわけで9割が完成しました。
パネル座標系の算出
後は Poincaré disk 上の座標を3次元空間内の座標に変換するだけです。データはあるのでアルゴリズムを考えます。
一応整理すると:
- プレイヤーの位置は Poincaré disk 上の座標で表現されている
- 空間自体が「滑る」ことがあるので、表示するときには
visualPos,visualRotで逆変換を噛ます - そうして得られた座標から、「乗っているパネルの番号」「パネル上のUV座標」を算出する ←ココ!
- これらを最初に作ったテクスチャと照合することで3次元空間内のフレームを算出できる
- あとはそこに椅子を置くだけ
こういう流れでした。
まず中央のパネルに対して UV 座標を計算する方法を考えます。元々のグリッドの作り方が「外周を等分し、対応する点を通る円弧を引く」というものだったので、これを逆に行えばいいはず。
が、これをどう求めればいいのかが自明ではありません。(Beltrami-Kleinモデルに持っていけば一瞬ということに気付いたのは後の話です)
なので最初は「対称の位置と自分を通る円弧を計算し、それと外周とが交差する点の角度を計算する」という方法を使っていました。
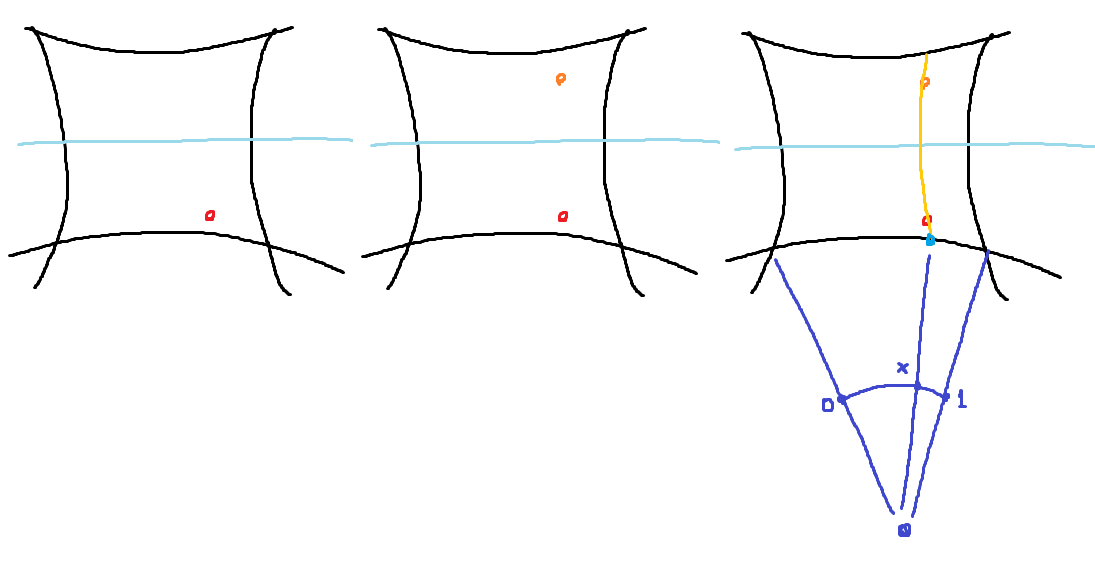
しかしこれでは対称軸に乗ってしまったときに条件が足りずうまくいきません!またもう一つの対称軸に乗ったときは円弧ではなく直線になってしまうので、円同士の交差判定も使ってはいけないはずです。
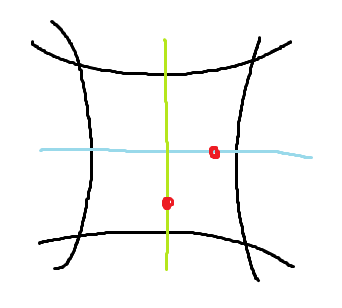
これによって「グリッドのローカル軸を跨ぐとアバターが一瞬吹っ飛ぶ」という問題が発生していました。困る。
そこで、まず対称点と自分との中点を求めることにしました。これはrobustに求まります。Gyrovector のめんどくさい足し算と引き算と掛け算をするとできます。
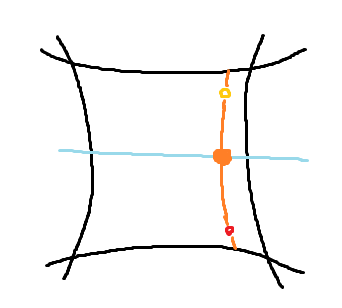
そして、そこから「縦に伸びる直線」と外周との交差点を取ります。ただし、このときにこの直線が円弧であることは使ってはいけません (本当に直線であることがあるため)。
どうしようかな~と思ったんですが、とりあえず方程式を建ててしまうことにしました。中点を 、対称軸と垂直方向を
、外周円の中心と半径を
として、
を
について解けば良いのです。
複素数なので変数の数がそこそこ多いように見えますが、実は は
上、
は
、
も
上にあるのでなんだかんだ単純です。
Wolfram | Alpha に投げたら解けました。
— phi16 (@phi16_) 2023年2月13日
というわけで衝突点がわかり、UV座標が求まりました。わーい。
さて中央以外のパネルについてですが、各パネルは全部合同です。つまり適当な変換をすれば中央のパネルとぴったり重なります。その変換 (pos, rot) は予めテクスチャに仕込んであるので、「パネルを指定すると、そのパネルが中央であるときの Poincaré disk 座標が得られる」状況です。そこから先程の計算を行えば「任意のパネルに対するUV座標」を計算できますね。
というわけで、残りの問題は「自分がどのパネルに居るのか」、だけです。
中央パネルから「少し」離れた場所で UV を計算すると、想像通り -0.1 とか 1.1 みたいな値が得られます。

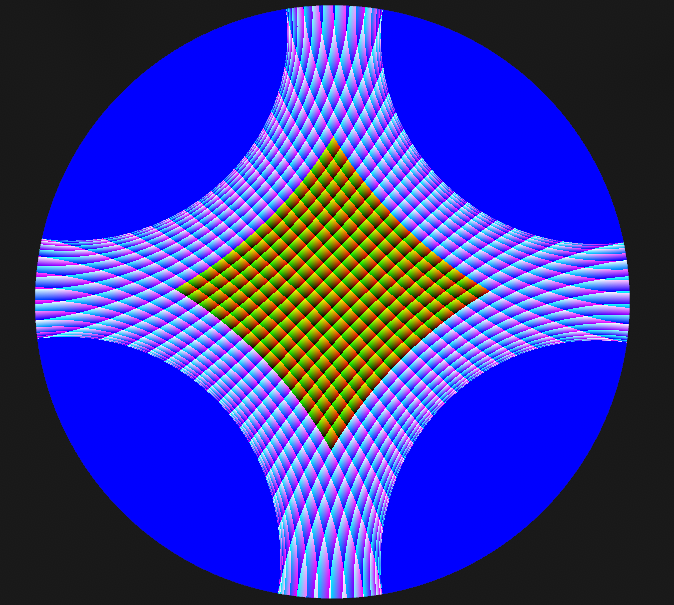
外側の青い区画でない領域に対しては正しくUVを計算できます。これを使えば「どちら側にはみ出ているか」を知ることができて、例えば「x < 0 なら現在のパネルの左に居るはず」ということがわかります。
各パネルはその上下左右に繋がっているパネルが何番であるかを知っています。よって「隣り合ったパネルに少しだけ移動した場合」はその番号に移動すればいいだけです。
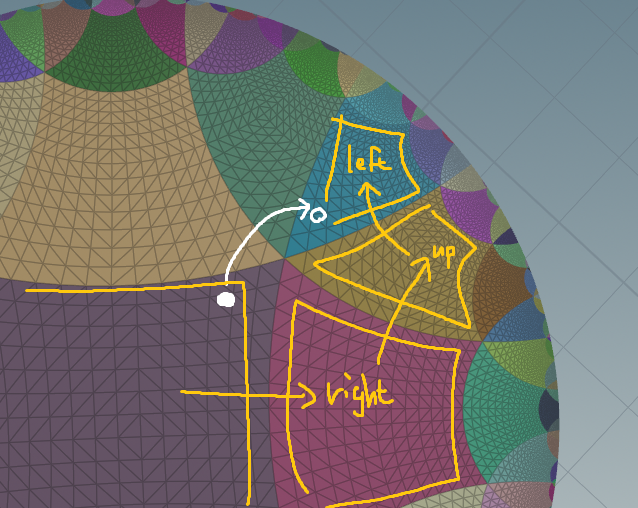
ちなみに角を通ってちょうど反対側に行ってしまうとパネルの移動を3回行わないと正しい位置にたどり着けません。なので念のため3回チェックするようにしました。
さて、で、青い区画 (UVが計算できてない場所) についてなんですが、正確なUVの値がわからなくても「なんか上に行けば/右に行けば辿り着きそう」であることはわかります。というわけでそっちっぽい方向にとりあえず移動すれば良い。
というわけで、「自分の居るパネルを管理しつつ」「そこから外れたら、そっちに移動」を繰り返すだけで適切なパネルに乗ることができます。
どうやら3フレームくらいあれば中央スタートから任意の場所のパネル番号が計算できることがわかりました。(グラフの直径が18未満ってことですね)
あとはまぁ座標から3次元的な位置を得るだけです。位置はまぁ bicubic 補間すれば手に入るのでいいんですが、姿勢がちょっと問題です。
位置を ∂/∂u, ∂/∂v で微分すれば (= bicubic 補間のときの係数をうまく調節すれば) 接空間が出てきます。しかしこれらは元々直交座標系ではありません。要は X 軸がどっち、みたいなことを言えないということです。
なので軸を定める必要があります。今回は ∂/∂v を X 軸にしました。まぁなんでもいいです。
プレイヤーの向きを一旦ローカルの ∂/∂v を X 軸とする座標系に回転させ、それを曲面上に転送、そして曲面上の ∂/∂v の方向と法線の方向から姿勢を計算しています。
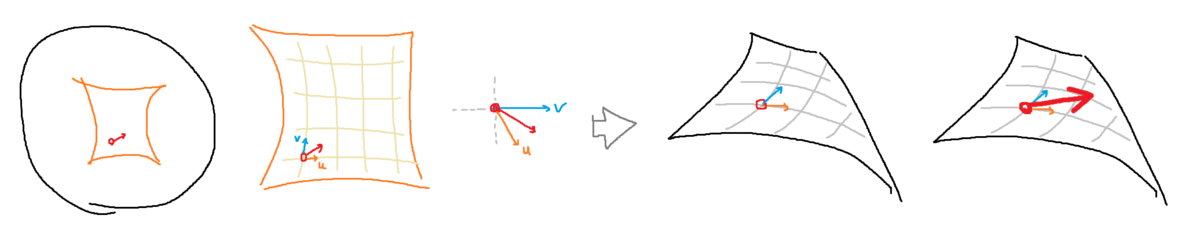
ちなみに、法線は ∂/∂u と ∂/∂v の外積で計算できますが、そしたらパネルとパネルの境界で不連続になってしまいました。まぁ確かに保証があるわけではない。
そこで法線もテクスチャにして参照するようにしました。

綺麗ですね。
(謎の放射方向の線は dilation 処理によるものです、円盤 (半径 0.975) 外を埋めるための。)
これで法線方向は連続に成ったんですが、でもまだY軸回転方向がほんの少しだけ不連続でした。∂/∂v の精度が足りないのかしら。
そこでもう連続になるように世界を回すということをしました。特に問題はありませんでした。
これでメイン構造についての解説はすべておしまいです。
模様の作り方

ぬるっと作った割にはめちゃいい感じです。
これを作った理由はまぁなんか賑やかしが欲しかったのと、Houdini 勉強会で出すにあたってテーマの「曲線」要素をもう少し回収しておこうという気持ちでした。
Poincaré disk 上の模様は円はそのまま円に移るので、円っぽい図形は勝手にいい感じになるはずです。処理もしやすそうかなって思った。
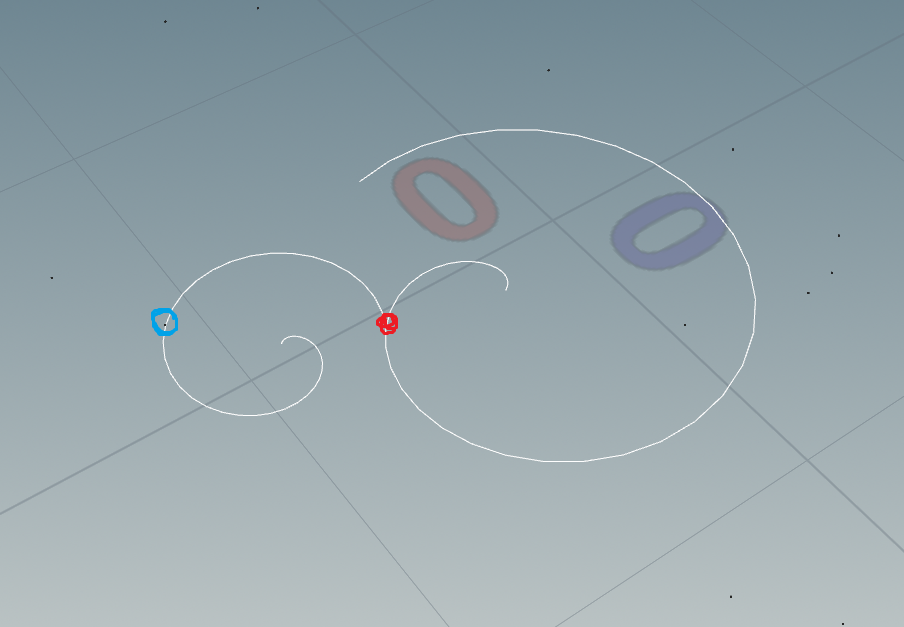
つくりかたです。
- Scatter で候補点を生やしておく
- 中央の1点を適当にマークする
- 以下を繰り返す
- マークされた点たちに近い候補点 (1~10番目とかでランダムに取りました) を選び出し、その最近マーク点 (赤) から最近候補点 (青) に向って渦巻きを生やす
- 赤点の進行方向に沿って半円を描く
- そのまま流れで クロソイド曲線 を描く
- 渦巻き上の点をすべてマークする
- 候補点がなくなったら終了
- マークされた点たちに近い候補点 (1~10番目とかでランダムに取りました) を選び出し、その最近マーク点 (赤) から最近候補点 (青) に向って渦巻きを生やす
めちゃ簡単に見えますね。これを素直に書けるHoudiniってすごい。
ほんとは渦巻きの生成をもっといろいろやろうと思ってたんですが、まぁ今の状態でもとりあえずは十分かなって思ったのでこうなりました。
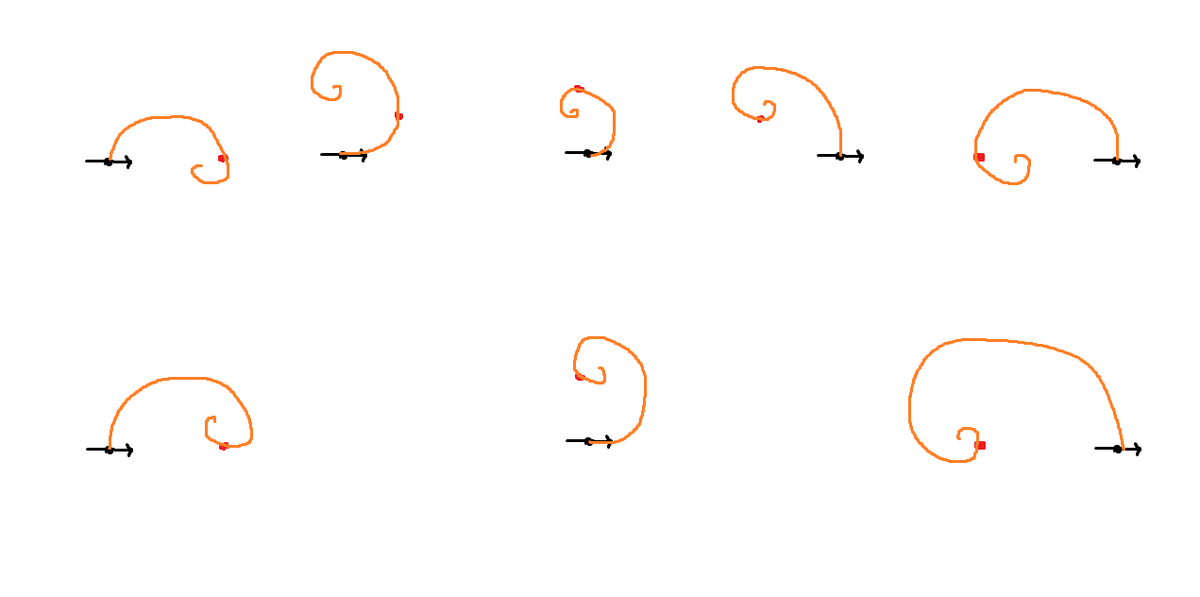
この生やし方だとトポロジーが 木 になってちょっと複雑性に欠けるかな?と思ってたんですが、パラメータ調節 (Scatter の Relax Iterations) でまぁいい感じになりました。
(ちなみに方法は違いますがこれについても 堀川さんがやってました。)
最後に、これをメッシュにするときに 計量 に気をつける必要があります。Poincaré disk の外側は圧縮されてるので、同様に線の幅も圧縮しなければなりません。
と言っても @pscale に を入れて Sweep するだけです。
が、逆に Y 軸は圧縮してはいけません (何故なら私達が扱ってる空間は ではなく
なので…)。
というわけで適当にもとに戻します。
これでメッシュは完成。
さて、これを3次元曲面に張るにはどうすればいいんでしょうか!
答えは「各頂点に対してパネル番号を追跡する」です。というわけでまず頂点位置をテクスチャに焼きます。

そしてシェーダでパネル追跡を実装して (このためにデータをすべてテクスチャにしていたのです)、CustomRenderTexture を回します。
できました。

というわけでこれですべて終わりです。お疲れ様でした。
ちゃんと文章にするとめちゃ長くなりますね…。
おわりに
いくらか加えてやりたいことはあって、例えば QvPen 使えるようにするとか、ボール投げられるとか…あるんですが、とりあえずこれで終えることにしました。やろうとすると完成しないので。
現状にはまぁ満足していますが、Beltrami-Klein モデルにしてグリッド計算を高速化するとか、Gyrovector の扱いをもう少しちゃんとしたいとかもあるので、次やるなら 1 から作り直すかもしれません。
なんとか異常空間が作れて良かったです。
おわり。
そういえば双曲空間に興味を持った方が居たら是非 Hyperbolica を遊んでください。
めちゃきもくておすすめです (ゲームとしておもしろいか?というとなんともいえない)。VR対応もしてます。