抽象というものは物事の共通部分を抜き出して、中にある本質的な構造を顕在化するものです。
「りんご1個」と「みかん1個」から「1」という概念を抽出するのが抽象というものです。
という写像を考えます。
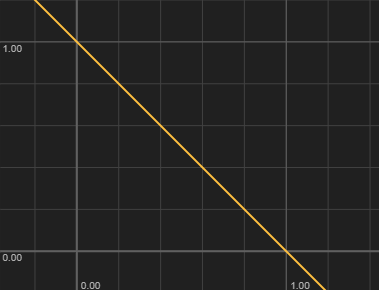
…これだけだと「意味」の考えようがないですけど、例えば横軸を時間、縦軸を位置として捉えれば:
こういう読み方ができます。左が0、右が1です。最初は右にいて 、最後は左
です。
さて、ここで という写像を考えます。これです:
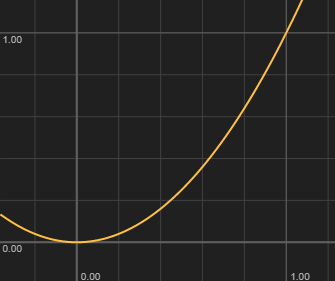
つまりこうです:
だんだん速くなる感じですね。
で。関数は合成することができます (一定条件を満たせば)。だから、例えば を考えることができます。それは:
こうなります。逆に、 を考えることもできて、そうすると:
こうなります。この2つはまぁ、みてわかるように、違うものです。その違いは、 を基準に考えるとちょっとわかりやすく読めます。
は、
の時間を反転させたもの (なのでだんだん遅くなる)
は、
つまり、ここでは が異なる意味で用いられています。同じ関数なのに。これは如何。
今の話では、 は「0から1の数」を「0から1の数」に写す関数として定義されていました。確かにそうです。
だけど、私達は意味を与えました。即ち、「時間」を「位置」に写す関数であると。そうすると、それに繋げる の役割も、合成の仕方によって変わってきます。
の入力、即ち時間に
を適用しています。
だから、自然に の棲む世界が変わっていたのです。時間を時間に写す関数と、位置を位置に写す関数。
ちゃんとそういう「棲む世界」を書いてあげると、次のようになります。
- 時間を表す空間
]
- 位置を表す空間
]
として、
を考える。
として、
を考える。
つまり。
意味を考えたことで (= 抽象へ向かう道筋の中で) 、同一視していたはずのものが、異なる2つのものに区別された、という現象が発生したのです。
だから抽象化はむやみに共通部分を抜き出すというわけではないわけです。見かけ上でしか共通でないものは、逆に区別していきます。
共通部分を取り出すことは共通でない部分、つまり具体的すぎる部分を忘れることです。だから、こうやって「 と
が等しいという見かけ上の関係」を忘れることがあるのです。
これは結局「そういう意味を考えたから」に過ぎないわけですが、まぁ、逆に言えばそれほどに「意味」「解釈」「視点」「願い」は重要だということです。
