Imaginantia

思ったことを書きます

最高の鍵盤について考える

ある音高の音を鳴らすという目的を叶えるUIのことを此処では「鍵盤」と呼ぶことにします。

私は良いUIで操作がしたかったので、いろんな試行錯誤をしてきました。

最終的にこれになりました (今現在)。始まりからここへ至る過程についての解説を書きます。

これは単に私が辿り着いた結論であり、「正しさ」を与えるようなものでは勿論ありません。

音程の持つ情報

まず音は波です。「音高を持つ」と呼ばれる音はある特定の周波数の波を多く含んでいます。

含んでいるだけではあるので一般に音から音高は「計算」できません。出来るのはスペクトルで見せることくらい。

そして波であるという点で、比が単純な波同士は綺麗に混ざるようにみえます。混ざるというのは人間の認知的な側面ですけど。

最も単純な比 1:2 はあまりにも綺麗でもはや「同じ音」とも言われてますね。確かに知覚上でもその通りです。

その次が 2:3 と 3:4 で、確かに綺麗。4:5 だとさすがに「違う音」ではありますが、綺麗に聴こえます。これらの感覚は基本原則として捉えてもそうおかしくないものだと私は思います。

というわけで、一応この比の感覚から始めて、諸々を組んでいきます。

歴史的経緯

比には既に多くの名前がついています。高々名前ではあるのでそう参照することは無いですが、一応。

  • 完全8度は 1:2 のこと。
  • 完全5度は 2:3 のこと。
  • 完全4度は 3:4 のこと。
  • 長3度は 4:5 のこと。

…いえ。この通りとは限らないんですが (後述) 、根底にある哲学はこれであるという信念で以てこれを記します。

「度」で数える世界と比で数える世界にはそこそこ隔たりがあることが見て取れます。この差が何よりも問題なのですが。

さて、古くからある概念で興味深いものがMajorとMinorで。特にそれらの三和音は3つの周波数の比からなる構造です。

  • Major Triad は 4:5:6 のこと。
  • Minor Triad は 1/6:1/5:1/4 のこと。つまり 10:12:15 のこと。

両端が 2:3 になってて、Majorでは前2つが 4:5、Minorでは後2つが 4:5 です。それだけの違いです。

これらは確かに綺麗に聴こえるんですが、それ以上に感情を持っていて。Majorは明るくて、Minorは暗い…まぁいろんな言い方はあるでしょう。

この2つの違いは明らかに重要です。それは理論的とかそういうのではなく、なんだかそう感じるのです。そういうものだと思います。

5を掛けるか割るかで違う感情が生まれる、ものすごいシステムですよね。素晴らしいです。

さて、とりあえずここまでの情報から考えられるUIの構造の1つが次です。

Lattice

en.wikipedia.org

つまり「右 4:6」と「左上 6:5」と「左下 5:4」で三角形を作ろうというわけです。上三角形はMajor、下三角形はMinor (逆にもできます)。美しいです。

しかし問題が2つあります。本質的には1つ…音高を比較できないことです。

この鍵盤では「調和する音」が綺麗に並びますが、「音が高い順」には並びません。愚直に 2:3 を守り続けると右3つ隣の時点で比は 8:27 となって 1:3 を越えます。

それを防ぐために「適切に 2:1 で戻す」ことが考えられますが、その選択は恣意的なものになってしまいます。

この辺について考えてた時期に作ってたのがこれですね。

f:id:phi16_ind:20201010224440p:plain

…見てもわかるものではありませんが。はい。

上三角形と下三角形の組み合わせは先述の通りLatticeなんですが、鳴る音はシェパードトーンになってます。呼び方は最近知りました。

つまり音に対する絶対的音程感を無くすことで戻す必要が無いようにしようとしたわけです。

でもダメだった。私はどうやら和音に対してもそこそこ絶対的音程を求めているらしかった、です。

まぁこういう音の作り方をしてしまうと制約がそこそこ掛かってしまうわけで、「望ましい」とは言えなかったのです。

…これで済めばそれで良かったんですけどね。左の6つの三角形は綺麗に左から Ⅱm, Ⅳ, Ⅵm, I, Ⅲm, Ⅴ になります。大体この辺、という話は聞いたわけですが…でも足りなかった。

もっと自由に音を出せる必要がありました。

音階

Latticeのもう一つの問題点が「順番に音を鳴らせない」ことです。ただ、これは「順番」の概念について丁寧に考えていく必要がまずありますね。

周波数は実数なので、明らかに順序が定まります。でも先程の「2:1 の違いを曖昧にする」考え方では世界はくるっと回って一周し、簡単に順序と呼べるものは定められません。

ただ、まず何故順番に音を鳴らしたいのかという話もあるんです。つまり私は何がしたいのか、です。

どうやら私の頭はそこそこ歴史的経緯を引きずっているようで、どうにも頭の中で音を並べたりすると確かに全音階になってるんです。

だからそこから向き合わないといけないのです。

先程の続きで考えると、全音階の配置は 1:1 8:9 4:5 3:4 2:3 3:5 8:15 1:2 です。一般にこれは純正律と呼ばれています。

しかしこの配置では D (8:9) に対しての 2:3 音程の音が存在しません。在るのは 16:27 ではなく 3:5 = 16.2:27 です。

この話は有名で…まぁどうしようもないんです。正しいので。

これは \log 5 は 1 と \log 2 と \log 3 の整数係数線形結合で表せないという意味。

これに対する一般的解決は、81/80 の差を等分してバレなくすることです。すると輪は綺麗に閉じ、平均律を成します。

ただもうちょっと抗ってみたかったので、もう少し考えました。

常に新しい音を生み続ければいいのではと。思って。

ある音を一旦鳴らしたとき、その音と調和する方に円を回り直すことが本来できるはずなんです。

つまり C 1:1 → G 2:3 → D 8:9 だけでなく、C 1:1 → A 3:5 → D 9:10 と出来れば調和度は上がると思って。

昔はこう、「機械」だったので気軽に周波数は変えられないわけですけどまぁ今ならできるわけじゃないですか。ね。

…みたいなことを思ってたんです。思ってたんですけど…根本的な問題として…私には81/80の違いはそうわからなかった。

勿論正弦波鳴らすとうなるのでわかるんです。もうちょっと複雑でも音が揺れるのでわかります。でも調和してないかというと、調和しているように聴こえるので。

…うむ。おとなしく平均律でいいやと思った。

まぁ実際これは困ることがあって、音を鳴らしていくと元の音に戻るとは限らないんですね。

気づいたら半音ぐらいずれちゃうかもしれない。一応変化は可逆ではありますが、制御可能ではありません。

もしも完全な制御能力と音程の認知が完璧な人が居たら何か違う結果にはなるのかもしれない。

あ、でも知覚できないからって無駄ではないんですよ。こういう音の自然さというのは恐らく全体的な旋律にも現れるものだと思っているので…どっち周りが近いのか、というのは何かの指標に成り得ると思います。適当なことを言っています。

この辺について考えてたのが先のツイートの右半分でした。

f:id:phi16_ind:20201010230322p:plain

これは左上から右に CDE、右下から左に FGAB です。くるくる回る。一本線が「半音」で二本線が「全音」です。わかりやすいですね。

Dを鳴らす直前が E, F, A なら 9:10、C, G, B なら 8:9 みたいなことを考えていた気がします。実は実装してないからわからないけど。

ちなみにさっきの三角形6つのUIで、左上の丸が 9:10 の D で、右下の丸が 8:9 の D でした。うねる。

以後も2つ D が出てきたときに違う音だったりすることがそこそこありますが、まぁ気持ち程度だと思います…。

そういえば 1:2 の差を明示的に示さなくても推測できたりしないかなと思って「近い方」を選択するようにしたりしたんですが…ダメね。

G → C で鳴らすと音が上がるようになっちゃいます。そうだね。

そこまで来るとやっぱり 1:2 音程の差はめちゃくちゃ大事なのだと実感してきました。同じ音なんかではないんです。同じ音だけど。

なのでその違いをちゃんと意識できる配置を以後考えていくことになります。

鍵盤としての配置

Latticeはしんどいです。だけどそれを前提として色々考えることはできます。

とりあえず全音階の8音が綺麗に収まることを念頭に、nanoPad2向けの配置を考えていました。

D A E B . ...
. F C G D ...

これはほぼLattice。音程の上げ下げの規則性が裏の四角で表されています。わからん。

これは横に 4:5、下に 9:8。左と右での同じ位置が 2:3 を成します。…いえ平均律になっちゃってるのでちょっと違いますね。

調和もするし順序もわかりやすいです。そうか？

D A E B    1 5 2 6
F C G D    3 7 4 8

元々1個ずらすようにしてたのを揃えてみたパターン。2個隣で全音程。左2下1で半音。左1上1も全音程です。

ちなみに別ボタンを押すと 1:2 上がったり下がったりします。うーむ。

割と音の順序がわかりやすくて実用的かなとさえ最初は思っていました。

 

…でもやっぱり違うんですよね。順序があるということは順番にならんでほしいのです。どうしても。

最終形

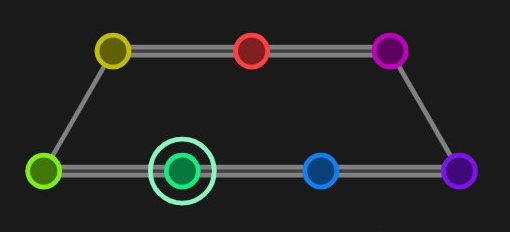
というわけで出来たのがこれです。

上に半音2つ、右上に半音7つ、右下に半音5つ。それぞれ 8:9 と 2:3 と 3:4 ですね、元は。

CDEと上に向かって縦に並び、その右の列でFGABと並びます。ある音の右には 1:2 の音があります。

真ん中のちょっと明るい領域が全音階の領域ですね。めちゃくちゃわかりやすい。うむ。

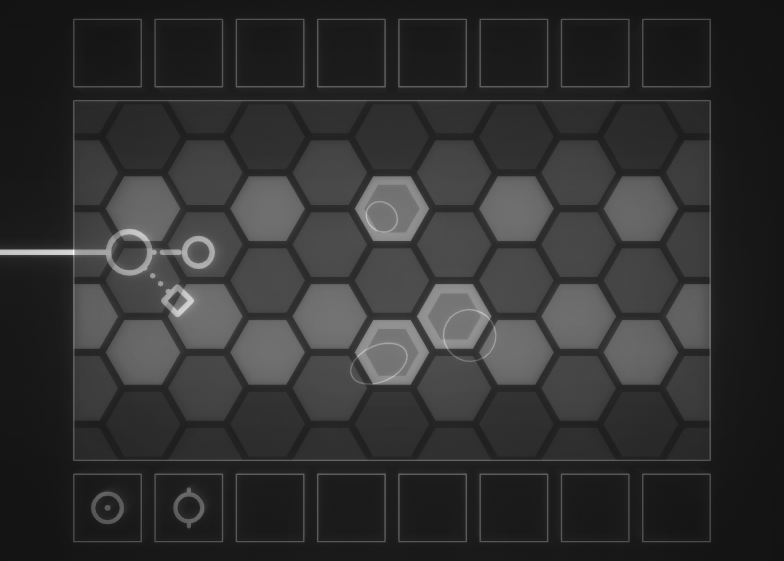
f:id:phi16_ind:20201010234635p:plain

2:3 もとい完全5度 (または 3:4 もとい完全4度) だと「波」ができます。そこにいい感じの場所 (上の浮島) に音を加えると Major Triad になります。これを上下逆でやると Minor です。

斜め3つ繋がっているのは 2:3 音程なので Suspended Chord になります。いっぱい鳴らすと透き通って綺麗。

…というわけで。調和性もわりと見やすくて順序が明らかで。わりと完璧なのでは。今の所めちゃくちゃ使いやすいです。

何よりも今までと違うのは「1:2 上の音がすぐ横にある」ことですね。気軽に上まで駆け上がったりできるようになった。

まぁこういう自由な配置が出来るようになったのはSenselのおかげでもあります。よいものを得た。

 

ちょっと純正律とかの話に戻ってみると、今回重要だったのはきっと「いい感じの場所」が波から離れていること、なんだと思います。

波が出来ている領域では 2 と 3 だけで出来た比の領域です。感情を表せる 5 を作り出すにはそこから離れないといけなかった。

ちなみにピタゴラス音律だと実際 E は 64:81 ですからね。さすがに 4:5 と言うべきでしょう。

そういう離れている感覚を適切に表すには「地続きな鍵盤」は相応しくなくてどうしようもない。だからこうやってUIの表示として「離れてる感」が出てるのはそれに対して相応しい対処なのかもしれません。

おまけ

ところでこの配置、どことなくピアノに似てませんか？

白鍵が3つと4つの領域を繰り返す感じ。ちょっと領域外に黒鍵がある感じ。

Latticeらへんについて考えてるときは弦楽器のE-A-D-G線とかにめちゃくちゃ納得したりもしたんですけど (これは全部 2:3 音程なんですね、合理的)。

「同時に鳴らすUI」としてはこういう調和音程が隣り合っているのは便利なのかもしれませんが、「順番に鳴らすUI」は全音程を横に置くスタイルに落ち着くのかもしれません。

間に黒鍵がない場所っていうのは実は近いんじゃなくて遠いんです。いえ音高的には近いんですが、調和的には遠いんです。つまり物理的には近いんですが、感覚的には遠いんだと思います。

1次元だとそういう感覚は適切に表現するのが難しい気持ちもありますが、2次元だと素直だった、というのが今回の結論かもしれません。

つまりあの配置は、合理的でないわけではないんですよ。時代背景とも絡まった複雑な合理性の果てなのだと思います。あんなに良い音を出す楽器ですからね…。

そこそこ論理的に実用的な結論に達せたし、それがある程度歴史的解法との親和性があるということで。色々考えてよかったという気持ちです。

 

まぁこれを自由に弾けるかどうかは全くの別問題ですけどね。

おしまい。

追記 0218

en.wikipedia.org

ありました。名前が。

つまりこれは「ある程度の正しさが示された」ということです。嬉しい。